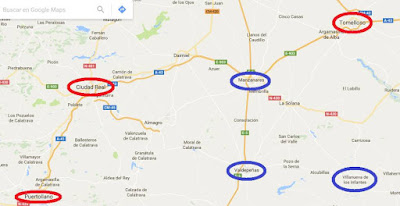
Tenir la possibilitat de viatjar de manera directa des de Puertollano a Valdepeñas, Manzanares i Villanueva de los Infantes quan l'ocasió ho requereixi. Algú altre, vol tenir la mateixa possibilitat, però viatja des de Ciudad Real, i tots dos saben d'una altra persona que desitja tenir la mateixa opció, però partint de Tomelloso. La situació de totes aquestes ciutats en el mapa es pot veure a la següent imatge:
És fàcil crear camins directes entre les ciutats que es volen connectar, però hi ha una condició a tenir en compte en aquest cas: no es poden trobar. Per tant, les carreteres que haurien de construir-se no poden tallar-se. Suposant que cap es construeix de forma elevada, com es podria resoldre aquest problema?
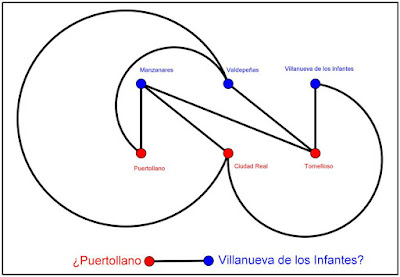
Bé, potser ordenant una mica les ciutats les coses es vegin millor. Si es representen cadascuna d'elles amb un punt i cadascuna de les carreteres amb una línia. Dibuixant-totes com segments, la cosa quedaria així:
Com es pot veure, en aquesta imatge les carreteres es tallen. La idea és que no es tallin, per la qual cosa caldria dibuixar alguna de les carreteres d'una altra manera (corba, poligonal ...).
Segur que en representar les ciutats amb punts i les carreteres amb línies, la situació hipotètica que es descrivia en els primers paràgrafs, ha portat d'un problema "geogràfic" a un problema de teoria de grafs.
S'haurà comprovat que no es pot fer el que s'ha plantejat al principi. Com a molt, es poden connectar dues ciutats d'un dels grups (el vermell, per exemple) amb les tres de l'altre grup i connectar la tercera ciutat del primer grup amb dos de l'altre grup, però faltaria una carretera per col·locar de manera que ja no es disposaria d'opció per evitar tallar amb alguna de les ja col·locades.
Per explicar la impossibilitat de realitzar aquesta construcció, cal ficar-se de ple en teoria de grafs. El graf que representa la situació que s'ha plantejat, el que apareix a la primera imatge, es coneix com
K3,3. La seva definició és precisament la que il·lustra el problema: dos grups diferents de tres vèrtexs cadascun (sense vèrtexs comuns) tals que cada un dels d'un grup està connectat només amb els tres de l'altre grup. És un cas particular dels grafs tipus
Km,n, que es defineixen de manera anàloga.
El que assegura que la construcció sigui impossible és que està demostrat que aquest graf no és pla (un graf és pla quan qualssevol dues arestes es tallen només en un vèrtex o no es tallen), i també està demostrat que
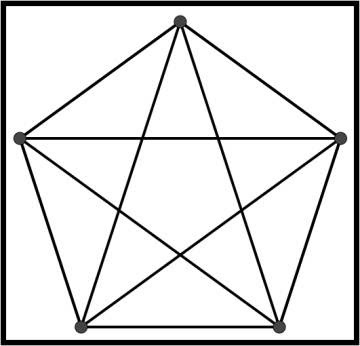
K5 (el graf de 5 vèrtexs en el qual cada vèrtex està connectat amb els altres quatre) tampoc és pla.
Com s'introdueix ara el graf
K5 en el joc? Encara que sembli que no té molt a veure amb el
K3,3, en realitat estan molt relacionats. Tots dos grafs són els protagonistes del conegut com teorema de
Kuratowski, demostrat pel matemàtic polonès Kazimierz Kuratowski en el 1930. Aquest teorema diu el següent:
"Un graf és pla si, i només si, no conté cap subgraf que sigui una subdivisió elemental de K3,3 o de K5"Com que no val la pena entrar ara en detalls pel que fa a això de subdivisió elemental , es deixa el teorema en què un graf és pla si no conté una part que sigui essencialment igual que
K3,3 o que
K5 . És a dir, aquest teorema diu, sense cap dubte, si un graf és pla o no ho és (és, per tant, una caracterització dels grafs plans ). En el nostre cas, com és el propi
K3,3, el graf que representa les carreteres per les quals es vol viatjar no és un graf pla, de manera que si es vol fer el que es demana en els primers paràgrafs no hi ha altra opció que deixar almenys un punt d'intersecció en el qual, encara que no agradi, es corre el perill de trobar-se.
I és igual el gran que sigui el graf en el que a vèrtexs i arestes es refereix: si hi ha
K3,3 o
K5, el graf no és pla; i si no es troba a cap d'ells, llavors el graf si és pla. Una altra cosa és el fàcil o difícil que sigui trobar algun d'aquests grafs de Kuratowski.
Font: Gaussianos