Proposem el següent petit experiment. És possible trobar una caixa que tingui totes les seves cares diferents a una llar?. No val una capsa de sabates, ja que les seves cares són (habitualment) iguals per parelles.
Possiblement no, ja que normalment les caixes que estan disponibles solen tenir totes forma de cuboide (la de sabates). Encara que pot ser que hagi estat possible localitzar-ne alguna amb una forma estranya que pugui servir com a exemple de caixa amb totes les seves cares diferents, ja que en realitat sí que es poden trobar caixes amb aquesta característica. Per exemple, es pot agafar un cuboide i tallar-li un trosset de la següent manera:
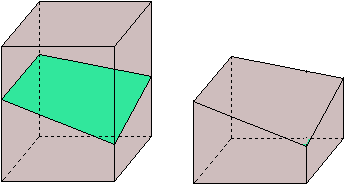 |
| Prisma1 | font: http://www.interaula.com/matweb/gespac/prisma/prisma.htm |
Evidentment, quan es parla de caixa en aquest context es vol dir poliedre (és a dir, una figura geomètrica en tres dimensions que les seves cares són planes (polígons) i el volum interior és finit) convex (és a dir, que compleix que tot segment que uneix dos punts del poliedre està contingut a l'interior del propi poliedre). Però pel que fa a que les seves cares siguin totes diferents cal afinar una mica més. S'ha vist que hi ha poliedres que tenen totes les seves cares diferents, però n’hi haurà que les cares siguin totes polígons amb un nombre diferent de costats? És a dir, buscar un poliedre on no es repeteixi cap polígon en el que a nombre de costats es refereix: que no hi hagi dos o més triangles, ni dos o més pentàgons, etc. Es pot trobar ara algun poliedre amb aquesta característica?
Abans de respondre intenteu que no influeixi la idea de regularitat polièdrica i pensar en la tremenda varietat que es pot trobar al món dels poliedres, i també en la barbaritat de polígons que es poden fer de cara d'un poliedre...
La resposta: no es pot trobar cap poliedre amb les cares siguin totes polígons amb números diferents de costats. Per demostrar-lo cal veure el llibre Mapes del metro i xarxes neuronals, de Claudi Alsina.
Suposant que es te un poliedre convex P que té un nombre de cares igual a C. S'¡anomena R a la quantitat de nombres naturals i per als quals el poliedre P té almenys una cara amb i arestes. Per exemple, un cub té R = 1, ja que només hi ha un nombre natural per al qual el cub té cares amb aquesta quantitat d'arestes: el 4. I anomenta ara K al nombre d'arestes que té la cara de P amb més arestes. En el cub que es tindrà K = 4, ja que aquesta és la major quantitat d'arestes que té una cara d'un cub.
Vegent un altre exemple per aclarir una mica més l'assumpte. Si Pés el prisma de base hexagonal que es pot veure a la dreta, es te que R = 2, ja que hi ha dos nombres naturals per als quals aquest prisma té almenys una cara amb aquestes quantitats d'arestes: el 4 i el 6. D'altra banda, K = 6 en aquest prisma, que és el major nombre d'arestes que té una cara del mateix.
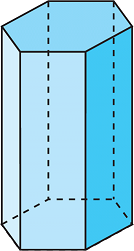 |
| Prisma 2 | font: http://www.interaula.com/matweb/gespac/prisma/prisma.htm |
Bé, aclarit això i jugant una mica amb aquests nombres. Evidentment P té almenys una cara amb K arestes (ja que K era el nombre màxim d'arestes que tenia una cara de P). Però cada aresta d'aquesta cara és també aresta d'una altra cara de P, el que dóna K cares més. Per tant, el nombre de cares de Pés, almenys, K +1 (la qual té K arestes més les K cares corresponents a aquestes arestes). Amb això s'arriba a la primera expressió interessant:
D'altra banda, les cares de P podran tenir 3 arestes (no poden tenir menys, no serien polígons), o 4 arestes, o 5, ..., o K (que era el nombre màxim d'arestes d'una cara de P). Si totes les cares tinguessin un nombre diferent de costats, tots aquests números serien algun del conjunt {3,4,5, ..., K}, conjunt en el que hi ha K-2 nombres. Però s'ha dit abans que R és la quantitat de nombres i per als quals hi ha una cara amb i arestes. Per tant R no pot ser més gran que K-2. I això dóna una segona relació
Que es pot escriure així:
Ja gairebé s'ha acabat. S'obtenen aquestes dues relacions:
D'elles s'obté el següent:
És a dir, ha de ser
Però, i aquí hi ha la clau, pensant en com seria tot això si el poliedre inicial tingués totes les seves cares amb un nombre diferent de costats. S'ha dit que C és el seu número de cares i que R és la quantitat de "números de costats diferents", és a dir, de nou el nombre de cares (recordar que s'està suposant que totes les cares tenen números de costats diferents). Això vol dir que en el poliedre hauria de ser C = R, expressió que entra en contradicció amb l'obtinguda fa uns instants,
La conclusió de tot això és que, com s'ha comentat abans, no hi ha políedres convexos en què totes les seves cares tinguin un nombre diferent de costats.
Font: Naukas


