Fem-nos la següent pregunta: Quina quantitat n de nombres enters aleatoris hem de prendre d'un interval [1, N] perquè la probabilitat que dos d'ells siguin iguals, sigui 1/2? La resposta és que n ha de ser aproximadament 1.18 √ N. Recordem que un nombre aleatori és aquell obtingut a l'atzar, i hi ha molts mètodes per generar-lo (per exemple, llençant monedes a l'aire).
Aquesta pregunta podria ser una d'aquestes que es fan els matemàtics i que podíem pensar que no serveixen per a res útil. No obstant això, la seva resposta té nombroses aplicacions pràctiques en la ciència de la computació i també en la criptografia, tal com mostrarem a continuació.
En aquesta entrada veurem un exemple de com els ordinadors poden detectar claus criptogràfiques i emmagatzemar missatges de manera correcta. En particular, el mètode que es descriu és el d'identificació d'una clau.
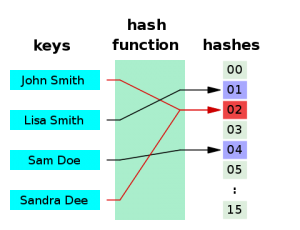
Un mètode comú d'identificació de claus és el mètode de les funcions hash. Una funció hashprodueix cadenes arbitràries de caràcters després d'introduir un missatge en una plataforma, per exemple, una clau alfanumèrica, de manera que no es pot crear aquesta cadena llevat que s'introdueixin les mateixes dades. Al conjunt d'entrades se l'anomena domini U de la funció hash. A un element d'U se l'anomena preimatge o, depenent del context, clau o missatge. El terme hash prové, aparentment, de l'analogia amb el significat estàndard en anglès d'aquesta paraula en el món real: picar i barrejar. Donald Knuth indica que encara que Hans Peter Luhn d'IBM sembla ser el primer que va utilitzar aquest concepte al 1953, el terme només hauria aparegut a la literatura a final dels anys 60 del segle XX.

Les funcions hash es fan servir per exemple per protegir contrasenyes, per garantir la integritat d'una descàrrega de dades, o per produir signatures digitals. No són pròpiament mètodes d'encriptació, sinó algoritmes.
Les funcions hash operen matemàticament com una funció f (x) que genera N resultats diferents i igualment probables. Si N és molt gran, sabem que després d'avaluar la funció en 1.18 √ N elements, tenim una probabilitat d'almenys ½ que f (x 1 ) = f (x 2 ).
Es diu col·lisió quan dues entrades diferents de la funció produeixen la mateixa sortida. El rang de la funció és finit, a causa de que la mida de les seves cadenes de sortida és fix. Per tant, la possibilitat de col·lisió no és nul·la. Una bona funció de hash és aquella en què les col·lisions són les mínimes. Es diu que la funció de hash serà perfecta si és injectiva, vol dir, que per cada dada d'entrada s'obté una cadena diferent. Perquè això passi, cal que la cardinalitat del conjunt domini sigui inferior o igual a la cardinalitat del conjunt imatge. Normalment, només es donen funcions hash perfectes quan les entrades estan preestablertes.

Les funcions hash, a més de per identificar claus, es poden utilitzar per comparar fitxers. Per exemple, la funció hash pot llegir els primers paràgrafs d'un fitxer i associar-los, similarment, cadenes alfanumèriques. Si obtenim la mateixa cadena, podem estar gairebé segurs que els fitxers són idèntics. Per què diem gairebé idèntics? El físic Bartolo Luque, professor de la Universitat Politècnica de Madrid, ens explica molt clarament la precisió de les funcions hash en el seu article El problema de l'aniversari i la seguretat de les nostres contrasenyes , publicat a la revista Investigación y ciencia. A continuació resumirem la seva explicació i convidem a llegir l'article complet, molt més detallat que aquesta breu entrada en seguretat i criptografia.
Luque diu gairebé perquè hi ha la possibilitat que es produeixi una col·lisió. Un tipus particular de funció hash produeix enfilalls de 160 caràcters de longitud. Aquestes seqüències poden representar-se en el sistema hexadecimal, amb base 16. Així, la nostra informació és capaç de proporcionar 2 160 = 10 48 sortides. A més, poden usar-se missatges amb una mida màxima de 264 bits, de manera que el nombre total d'arguments possibles és de 10 3x 10 ^ 18, un nombre immens. El nombre d'entrades és immensament més gran que el nombre de sortides, el que suggereix que moltes entrades generaran el mateix resultat.
Un petit càlcul, tornant al problema del paràgraf inicial, ens dóna que per obtenir una col·lisió amb probabilitat ½, aplicant l'aproximació de [1, N = 10 48 ], obtindrem n = 1.18 x 10 24nombres aleatoris generables en l'interval. Com veiem, la funció hash gaudeix d'una injectivitat prou fiable com perquè nombroses pàgines web xifren amb elles les seves bases de dades. Per a un pirata informàtic seria una tasca àrdua desxifrar les nostres contrasenyes, ja que els exigiria trobar totes les entrades que produïssin un mateix hash o missatge.
Font: Matemàtiques i les seves fronteres
