En els quadrats màgics numèrics, no sempre es compleix que tots els nombres són diferents. És evident que si tots els números són iguals, el quadrat resultant és trivialment màgic, però repetint només alguns apareixen també coses interessants. Un dels exemples més coneguts d'aquest tipus de quadrats màgics és que apareix en l'anomenada Façana de la Passió de la Sagrada Família de Barcelona. És aquest:
 |
| Quadrat màgic de la Sagrada Família |
A part que hi ha algun nombre repetit, i que totes les files, totes les columnes i les dues diagonals sumen 33, en aquest quadrat màgic hi ha moltes més combinacions numèriques que sumen aquesta quantitat. A la imatge es poden veure algunes d'elles, però hi ha més.
Tornant als quadrats amb nombres diferents, per exemple un només amb nombres primers. N'hi ha, i amb nombres primers consecutius. Aquí n'hi ha un que conté tots els nombres primers des del 79 fins al 439, la constant màgica (suma de files, columnes i diagonals) és 2016:
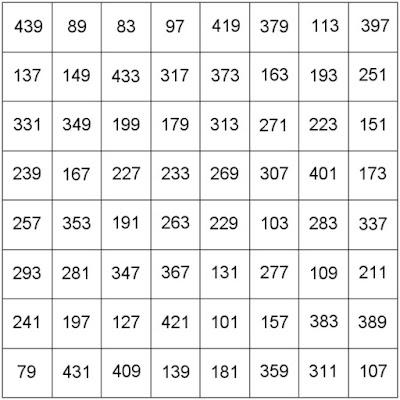 |
| Quadrat màgic de cosins consecutius amb constant màgica 2016 |
En el Magic Square with Sequential Prime Numbers es poden veure altres quadrats màgics de diferents mides que contenen nombres primers consecutius.
Fins ara, en tots els quadrats màgics que s'han presentat, l'operació que es fa servir és la suma. Es poden trobar quadrats màgics relacionats amb una altra operació? Doncs sí, hi ha quadrats màgics de productes. És a dir, quadrats màgics en què totes les files, totes les columnes i les dues diagonals donen el mateix resultat en multiplicar els seus termes.
Però n'hi ha més grans, per exemple un d'ordre 8 que compleix que totes les seves files, totes les seves columnes i les dues diagonals tenen com a producte el nombre 2058068231856000:
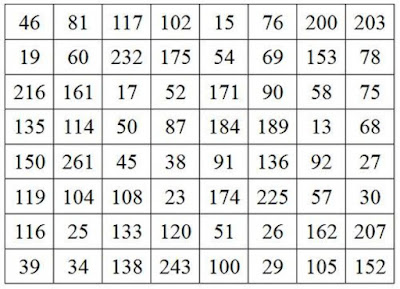 |
| Doble quadrat màgic sumes-productes |
Sumant totes les les seves files, totes sumen 840. I quan es sumen les seves columnes i diagonals, donen 840. Això es un quadrat numèric d'ordre 8 que és màgic per sumes i també per a productes.
Aquests quadrats que són màgics per sumes i productes no són els únics que desborden màgia per a dues operacions.
Les seves files, les columnes i les diagonals sumen 260. Ara, col·locant en cada casella el quadrat de cada número i sumant les files, les columnes i les diagonal, totes sumen 11180. Això vol dir que s'està davant d'un quadrat màgic que dóna un altre quadrat màgic en elevar tots els seus termes a 2.
El següent quadrat, va ser creat per Benjamin Franklin:
Si es sumen les files i les columnes, el resultat és 260, però les diagonals sumen un altre número. Doncs tampoc és tan rellevant com per citar-lo aquí. Sumant les cantonades, dóna 130, la meitat de 260. Sumant els quatre nombres centrals, i també dóna 130. Ara prenent qualsevol quadrat de quatre números, el que es vulgui i si es sumen els seus elements, el resultat és, 130. I una més (possiblement no l'única). Si es sumen els quatre elements de la diagonal ascendent 50-8-7-54 i al resultat es suma el que dóna la suma dels quatre d'elements de la corresponent diagonal descendent, 43-26-25-47, el resultat és 260. Bé, doncs això funciona en tots els casos, tant si es comença amb ascendent i es segueix amb descendent com si es fa al contrari.
Amb un d'ordre 13. Concretament aquest:
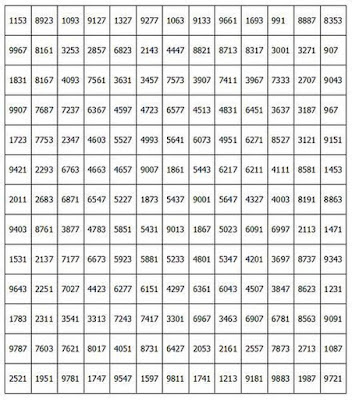 |
| Quadrat "polimágic" |
La seva constant màgica és 70681. Prenent ara el quadrat d'ordre 3 central i sumant files, columnes i diagonals ... també és un quadrat màgic. Bé, prenent ara el d'ordre 5 central ... també és un quadrat màgic, i el d'ordre 7, i el d'ordre 9, i també el d'ordre 11. Però ho és encara més si es sap que la constant màgica de cada un d'ells difereix en 10874 respecte de la de l'anterior. És a dir, la del d'ordre 11 és 70.681-10.874 = 59.807; la del d'ordre 9 és 59.807-10.874 = 48933; la del d'ordre 7 és 48.933-10.874 = 38059; la del quadrat d'ordre 5 és 38.059-10.874 = 27185; i la del d'ordre 3 és 27.185-10.874 = 16311.
S'han vist quadrats màgics amb nombres primers, alguns que barregen diferents operacions i altres amb algunes propietats realment interessants i curioses, però tots estan relacionats directament amb nombres. Amb que més podien estar-ho? Doncs amb la geometria. També hi ha quadrats màgics amb figures geomètriques, anomenats quadrats geomàgics, com aquests:
En aquest
enllaç, n'hi ha molts més.
Per finalitzar, l'últim tipus de quadrat màgic és el quadrat d'àrees màgiques. En ell, cada regió té d'àrea el nombre que inclou, i el resultat dóna un quadrat màgic habitual (files, columnes i diagonals sumen el mateix). Tot seguit hi ha un exemple perquè es vegi millor.
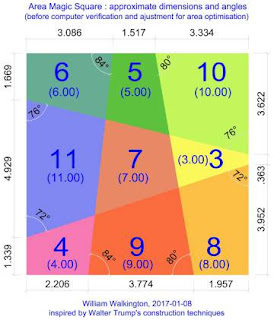 |
| Quadrat d'àrees màgiques |
Una preciosa manera de relacionar els quadrats màgics numèrics amb la geometria sobre la qual es pot trobar més informació a
Àrea Magic Squares and Tori of Order-3.
Font: Gaussianos 




