En ocasions, els estudis i treballs matemàtics es consideren innecessaris, prescindibles o una pèrdua de temps al·ludint, principalment, falta d'utilitat o nul·les aplicacions pràctiques dels mateixos. Un cas que exemplifica que aquests estudis són necessaris, encara que al principi no se'ls vegi una aplicació pràctica, ja que mai se sap quan ni on podrem trobar-los utilitat, són les antenes parabòliques. La seva forma no fa referència a una qüestió estètica ni a un caprici d'algun fabricant, sinó que respon a una qüestió merament matemàtica que, concretament, fa servir de manera molt intel·ligent una propietat de les paràboles coneguda des de fa gairebé 2000 anys.

Primer de tot, recordar què són les paràboles. Una paràbola és una cònica (corba que sorgeix de fer un cert tall a un con) que es defineix com el conjunt de punts que estan a la mateixa distància d'un punt concret, anomenat focus, i una certa recta, anomenada directriu. A la següent imatge podeu veure una paràbola (en vermell), el seu focus i la seva directriu i la igualtat de distàncies a aquests dos objectes des de diversos punts de la mateixa:
Llegenda: Paràbola. Les distàncies dels seus punts al focus i a la directriu són iguals.
A partir d'aquesta definició, és fàcil construir un objecte en 3D girant la paràbola respecte d'un eix vertical que passa pel seu focus. En fer això, obtenim una superfície tridimensional anomenada paraboloide:
Llegenda: Paraboloide. Es mostren també el seu focus i una paràbola que el genera.
S'acaba de crear una antena parabòlica. El focus és el mateix que el de la paràbola que s'ha girat.
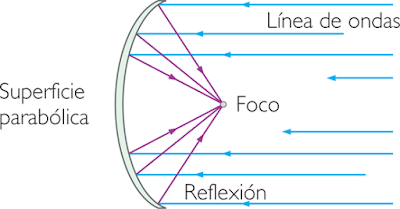
Per què és útil aquesta forma? Doncs per una interessant propietat de les paràboles que es descriu a continuació: “Un punt de l'interior de la paràbola que es mogui per una recta paral·lela a l'eix rebotarà a la paràbola i serà enviat cap al focus”.
Això vol dir que si s'envien senyals cap a la paràbola que siguin paral·leles a l'eix, aquestes seran reflectides per ella cap al focus, independentment de la recta que s'usi. en aquest enllaç hi ha una demostració, atribuïda a Dositeo. Una mostra gràfica per veure-ho de forma animada. I això és molt útil, ja que amb un paraboloide que tingui un receptor de senyal col·locat en el focus, es pot aconseguir que tots els senyals que reboten en el paraboloide acabin essent enviats a aquest receptor, sense necessitat d'haver d’apuntar directament a aquest. És a dir, amb un petit receptor obtenim una gran recepció de senyal utilitzant tota la superfície del paraboloide de la forma descrita.
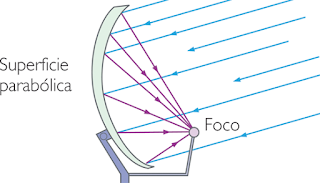
Aquesta propietat no es fa servir per a les antenes parabòliques, sinó per a altres dispositius, com cuines solars. Es construeix un paraboloide que reflecteixi els raigs del sol i es col·loca en el seu focus l'objecte a cuinar, aconseguint així que s'escalfi molt més ràpid. Això també pot usar-se per acumular energia solar, col·locant un acumulador en el focus del paraboloide.
D'altra banda, aquesta propietat també es pot utilitzar de manera inversa si es col·loca en el focus del paraboloide un emissor de senyal orientat cap al paraboloide i s'emet aquest senyal cap a la major part possible de la seva superfície. Tots els senyals "rebotaran" en la mateixa i es reflectirà de forma paral·lela al seu eix cap a fora, aconseguint així major emissió de senyal que la que obtindríem emetent només des d'un punt. Per exemple, això es pot fer servir en fars de vehicles (col·locant una bombeta en el focus per emetre major quantitat de llum) o a micròfons parabòlics (amb un micròfon en el focus per emetre so a major superfície).
Per què les antenes parabòliques són parabòliques?
I per finalitzar, una altra curiositat. Com es pot veure a la imatge principal que il·lustra aquest article, el focus del paraboloide està subjecte amb quatre barres rectes que es recolzen en la superfície del mateix (cal subjectar d'alguna manera). Això té el problema que alguns senyals, tant si emetem com si rebem, poden rebotar en aquestes barres i, per tant, perdre’ls. Per evitar això, el que es fa en algunes ocasions és prendre per l'antena una part del paraboloide que no estigui a sota del focus, sinó a un costat, com es veu també en les dues antenes que apareixen a la dreta en la imatge principal, o a la que es pot veure a la dreta. Així s'eviten aquests rebots en les subjeccions, i s'aconsegueix una antena més eficient.

Com es pot veure, estudis que al principi es fan sense pensar en possibles usos, acaben trobant aplicacions pràctiques molt interessants i útils que, en aquest cas, han suposat un gran desenvolupament en molts camps. Per això, seria ideal no subestimar els estudis matemàtics, per molt abstractes que ens semblin. Mai se sap quan poden ser d'ajuda en el dia a dia.
Font: Gaussianos
