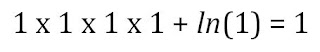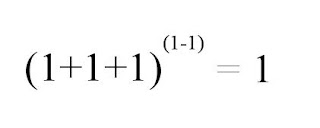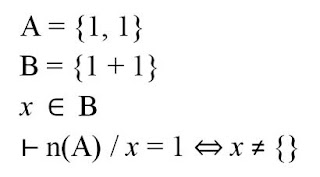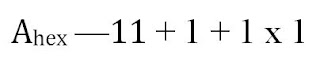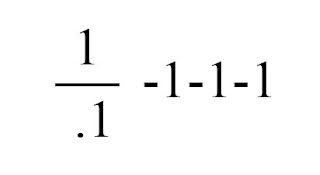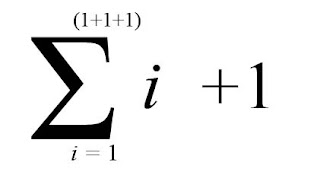Aquest és un problema simple i divertit; és una mica vell però sempre hi ha la possibilitat que no s'hagi vist mai abans.
El problema és com segueix: Es tenen a la nostra disposició cinc uns, que es poden usar de qualsevol forma que es consideri necessària. Amb aquestes cinc unitats, s'han de construir els nombres de l'1 al 10, i es poden usar els signes matemàtics de les operacions que es vulguin (suma, resta, arrel quadrada, etc.), però no es te suport de cap altre nombre. Per utilitzar el 0, cal posar (1-1); per fer un exponent al quadrat, es posa (1 + 1). Sí que es poden ajuntar, com 11, 111, etc.
Per exemple: 1 x 1 x 1 x 1 x 1 = 1,
o bé: (1 + 1) / (1 + 1) x 1 = 1,
i també: (11/11) x 1 = 1.
En tots aquests exemples s'està fent servir un 1 extra (el costat dret de la igualtat) simplement per demostrar que l'operació és vàlida. Ara bé, de l'1 al 5 les respostes immediates són trivials, perquè els cinc números poden ser construïts usant únicament suma i multiplicació. Per descomptat, es pot intentar construir-los de formes més imaginatives, per exemple:
(El logaritme natural d'1 és 0).
O bé: (Qualsevol nombre elevat a la potència 0 és 1).
Si es vol posar molt exòtic i utilitzar notació de teoria de conjunts, es pot fer alguna cosa com:
Encara que aquí, la veritat, ens estem passant una mica. Però es pot intentar fer alguna cosa més decent que això. I si vostè és un
friki total, pot considerar operacions incloent notació hexadecimal:
(El 10 en notació hexadecimal s'escriu Ahex ).
Així es pot passar una bona estona tan sols amb l'1, però si se segueix només amb operacions senzilles, les coses són més interessants del 8 al 10, perquè necessàriament cal usar exponents i agrupacions amb parèntesis. No obstant això segueixen sent molt simples de trobar.
Però és clar, d'això no tracta el test. De l'1 al 10, el número 7 és l'excepció: cal pensar una mica més per trobar-lo, perquè la forma de construir-lo no és tan immediatament aparent com les dels seus nou col·legues.
Més avall posarem tres formes diferents d'arribar al 7 usant els esmentats cinc 1, ordenades de menys a més creativitat, però preneu-vos una estona per veure si es poden trobar solucions abans de veure-les.
El problema pot ser trobar una expressió per a l'operació 10-3. Aquí hi ha una forma de fer-ho:
Aquí hi ha una segona solució, més creativa, que el que fa és trobar 6 + 1:
Que vol dir "la sumatòria de tots els valors de i , on i va des d'1 fins a 3, més 1".
I finalment una manera més creativa encara:
Si es verifiquen de nou les regles, es veurà que és vàlida.
Font: Naukas